其实关于这个知识点,有一则很通俗有趣的传说:
很久以前,一个村庄里住着一位退隐的大侠,相传大侠的剑法非常高明。
在一个月黑风高的夜晚,魔鬼抓走了大侠的妻子。大侠取出尘封多年的剑,来到魔鬼的城堡要救他的妻子。但是魔鬼却提出要求,要和他玩一个游戏。
魔鬼在桌子上放了两种颜色的球,说:“用你手中的剑分开它们,要求是尽量在放更多球之后,仍然适用。”
大侠拔出利剑一挥,桌上出现一道裂痕,准确地分开了两种球。
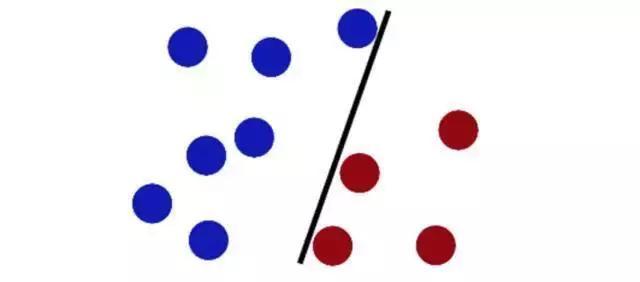
然后魔鬼又在桌上放了更多的球,大侠如法炮制,手起刀落,虽然有一个球没有准确划分,但依然干得漂亮。
大侠发现,剑痕的最佳位置,就是让剑痕离两边的球都有尽可能大的间隙。
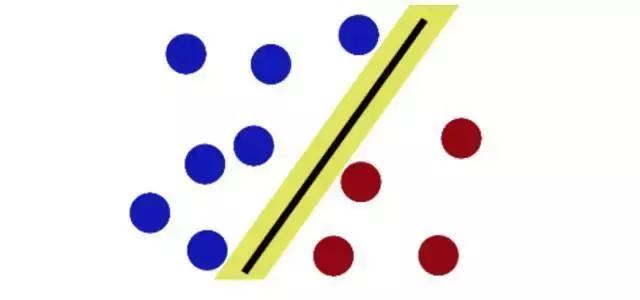
有了这样的思想,现在即使魔鬼放了再多的球,就仍然能够很好地划出分界线。
当然,魔鬼不会善罢甘休,于是把一堆球随手一扔:把它们分开。

大侠看到这样摆放的球,也是有点懵逼的。就在魔鬼开启嘲讽模式时,大侠想到了新的办法。
他左手在桌上一拍,球飞到空中。然后,凌空腾起,用手中的剑划出一道光波,恰好穿过两种球的中间。
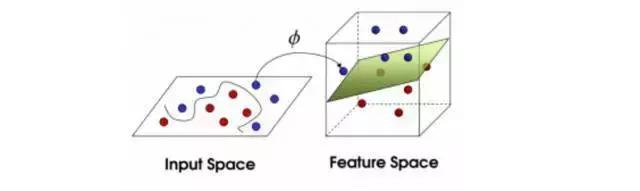
从魔鬼的角度看这些球,它们看起来像是被一条曲线分开了。
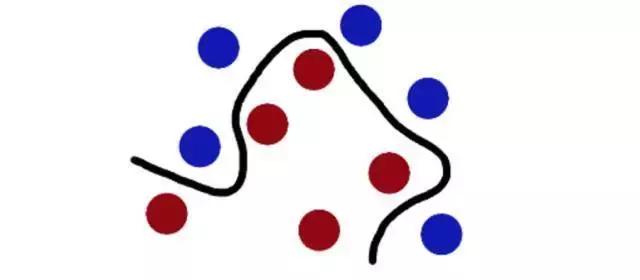
大侠救回了妻子,然后故事在村里传开了,并被杜撰成了美丽的故事。也就成了现在的支持向量机传说。
听完这个故事,是不是对支持向量机有了一些更加感性的认知?
今天,班主任就来给大家详细讲一讲线性支持向量机问题。
支持向量机SVM
支持向量机(Support Vector Machine,以下简称SVM)主要用于解决模式识别领域中的数据分类问题,它属于有监督学习算法的一种。
SVM要解决的问题可以用一个经典的二分类问题加以描述,也就是我们在开头讲的那则传说。如图a所示,在二维坐标中有一堆红色的球和蓝色的球,能否用一条直线将它们分开呢?显然是可以的,而且满足这一条件的直线也显然不止一条。
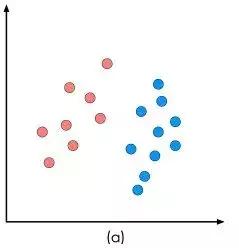
这类问题在模式识别领域称为线性可分问题。
支持向量
图b和c分别给出了两种不同的分类方案,其中黑色实线为分界线,称为“决策面”。
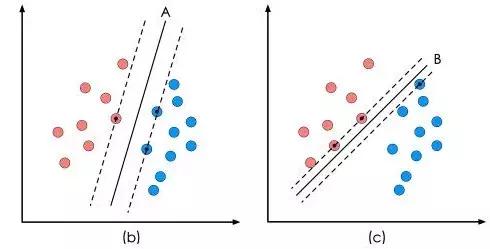
不同的分类器(比如说决策树、神经网络,逻辑回归)会给出不同的分类边界,而它们都是在找一个“最好的”的决策边界。SVM的意义也是如此。
以图(b)为例,虚线的位置由决策面的方向和距离决策面最近的几个样本的位置决定。两条虚线之间的垂直距离,就是这个决策面对应的分类间隔。
显然,每一个可能把数据集正确分开的方向都有一个最优决策面。而不同方向最优决策面,它们的分类间隔通常是不同的。那个具有“最大间隔”的决策面就是SVM要寻找的最优解。而这个最优解对应的两侧虚线所穿过的样本点,就是SVM中的支持样本点,称为支持向量。
回到图(b)中的数据,A决策面就是SVM寻找的最优解,而相应的三个位于虚线上的样本点,在坐标系中对应的向量就叫做支持向量。

最佳决策边界
那么如何判断一个决策边界好呢?让我们来看一下SVM的关键假设:决策边界两边最近的样本到决策边界的间隔最大,此时的决策边界为最佳决策边界。
间隔
以上举例为二维平面中的例子。而在样本空间中,划分超平面可通过如下线性方程来描述:
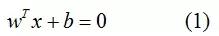
其中w为法向量,决定了超平面的方向;b为位移量,决定了超平面与原点的距离。而对于训练样本(xi,yi),则满足以下公式:
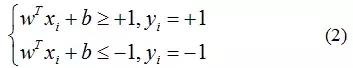
公式(2)称为最大间隔假设,yi=+1 表示样本为正样本,yi=−1 表示样本为负样本。
再经过一系列的变形,可以求出间隔的最终表达式
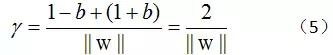
间隔最大化
SVM的思想是使得间隔最大化,也就是:
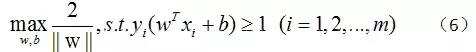
显然,最大化 2||w|| 相当于最小化 ||w||,公式(6)可以转化成:
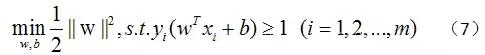
公式(7)即为支持向量机的基本型。
对偶问题的解决方法——拉格朗日乘子式
看到这类带约束的最小值问题,很自然我们想到了拉格朗日乘子法。
由此最终求解可以得到模型:
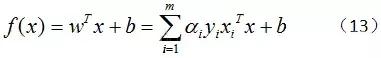
从这个结论里我们可以看出支持向量机的重要特征:当训练完成后,大部分样本都不需要保留,最终模型只与支持向量有关。
应用场景
近年来SVM已经在图像识别、信号处理、基因图谱识别等方面得到了广泛的应用,例如在无人驾驶技术中,需要对路面箭头指示进行识别,这里就用到了SVM。

又比如,方向梯度直方图(Histogram of Oriented Gradient, HOG)特征是一种在计算机视觉和图像处理中,进行物体检测的特征描述子。如今,HOG特征结合SVM分类器已经被广泛应用于图像识别中,尤其是在行人检测中,获得了极大的成功。
支持向量机 VS 深度学习
SVM和深度学习(DeepLearning,以下简称DL)相比,有哪些特点和适用场景呢?
一般来说,SVM在解决中小数据规模(相对少)、非线性(惩罚变量)、高维(核函数)模式识别方面,具有较大的优势。DL处理的对象主要为图像和声音,其优势在于对原始特征的表示。
但是神经网络相当于一个黑盒模型,在一些关键的应用场合,会有较高的风险。
例如在智能医疗方面,一个医生使用了基于深度学习的系统,却由于神经网络的“黑盒”特性,无法向患者解释诊断原理,那用户极有可能会因为高风险而拒绝。
